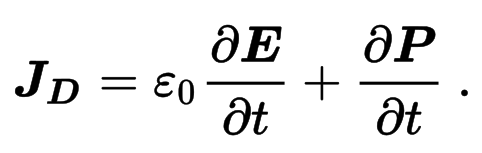Displacement Currents

Kirchhoff’s Broken Law?

Ever wonder why the current at the end of a dipole antenna isn’t quite zero? Ever wonder why the current in the red wire in this diagram…

…can have a current equal to the right side of the transformer even though the current has no where to go?

The good news is the current does have somewhere to go thanks to…

Energy Storage via Displacement Current

Griffith brilliantly summarizes this very important reality…

…we recall the rule known as Kirchhoff’s current equation [. . .]. This rule states that the sum of all currents entering and leaving a given branch point in a network must equal zero.  Figure 38-1 illustrates this principle.  Here we have a branch point with several currents flowing in and out, and the sum of all the inflowing currents must exactly equal the sum of the outflowing currents. We can explain this line of reasoning further by enclosing the branch point in a volume, whose boundary is represented in the figure by the dashed line.  Now we can say that the sum of all currents crossing the boundary of this volume must be zero.  And it makes no difference whether the volume encloses a branch point or a telephone exchange; the currents will still total zero. Speaking from a more fundamental mathematical standpoint, we should say that the integral of current density over the entire boundary area of any volume must equal zero. [. . .]  Current cannot just accumulate in a volume; what goes in must come out.[2]

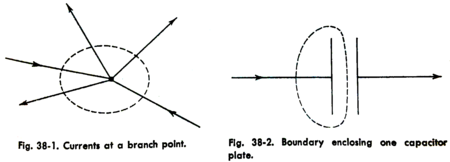
Suppose we now select a volume which encloses one plate of a capacitor but not the other; the boundary surface of this volume passes between the plates, as is shown in Figure 38-2. We see that current is entering the volume through the wire on the left-hand side, but there doesn’t seem to be any way for it to get out. How does our theory fit into this situation?

The answer to this becomes clear when we consider what is happening in the dielectric region between the plates of the capacitor. As current flows into the capacitor, charge accumulates on the plates, and the voltage across the capacitor rises.  This means that the E field in the dielectric is increasing, and therefore the dielectric displacement D is also increasing. Thus we can see that, in order to satisfy the Kirchhoff current equation, there must exist in the dielectric material a displacement current which is proportional to the rate of change of the dielectric displacement D. If we consider the displacement D to be the density of electric flux, we may consider the displacement current to be a flowing-in of additional flux as required when the density is increased. Whatever it may consist of, the total displacement current in the dielectric region will exactly equal the conduction current which is flowing into the volume through the wire.[2]

Bold emphasis added. Thanks to displacement currents at the antenna end charging the dipole’s capacitance and creating an e-field…

 

…Kirchhoff’s current law is happily maintained and all is well with the antenna world.

Three kinds of current

Displacement current along with drift and conduction currents provide the necessary concepts for the EE to understand antenna behavior. This video helps understand all three…

Conclusion

References

1. “The End Fed Half Wave Antenna” – Steve Yates, AA5TB
2. Griffith, B. Whitfield (1962). Radio-Electronic Transmission Fundamentals. New York, NY: McGraw Hill Book Company, Inc. pp. 318–320.