Coax Velocity Factor in Baluns, Does it Matter? Part 1

Quarter Waves and Velocity Factor

Numerous folks use baluns for their antenna feedpoints. Toroid chokes are wideband and popular in the HF frequencies.

VHF and UHF antennas, especially beams, often have balanced feed points. Several methods exist to connect unbalanced coax to the dipole element: gamma, t-match, etc. Some VHF/UHF Balun options use tuned stub or shunt topologies to achieve the unbalanced to balanced goal; Methods include the Pawsey Stub, Split Coax Balun, Coaxial Cable Balun and Folded Balun to name a few. Each of these requires specific lengths of conductors based on multiples of 1/4 wavelength at the design frequency.

When calculating 1/4 wavelengths, however, it seems the amateur radio community has lost the collective knowledge of when Velocity Factor (VF) of Coaxial Cable Dielectric Material applies. Indeed despite the decades of college texts and ARRL Antenna books showing otherwise, the idea Velocity Factor always applies to coaxial cable length calculations when used as nothing more than a wire stub in a Balun seems to have gone viral on the Internet.

The web site of G0KSC provides innovative computer simulation refinements to the classic Coplanar Loop Fed Yagi-Uda design. The author focuses on the topic of Baluns on his questionable Creating a Balun web page.

The topic of Baluns is vast so let’s just focus on the ones for VHF/UHF antennas. Often these are tuned assemblies using some combination of coax and/or wire stubs of specific lengths.

G0KSC highlights several Baluns on his web page:

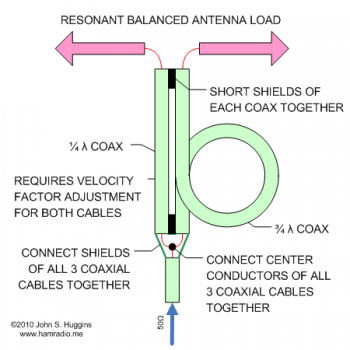
• 1:1 Coaxial Cable Balun I have never seen before using 1/4 and 3/4 wavelengths of coax. This is similar to the 4:1 Balun we have seen for decades in the literature.
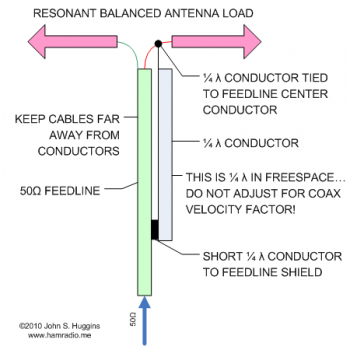
• 1:1 Pawsey Stub – a method using a 1/4 wavelength wire off the coax center conductor and tied a 1/4 wavelength back.

One comment made on the web site concerns velocity factor of coax. Certainly the Coaxial Cable Balun has this effect which requires shortening wavelength dependent coax pieces. The author also claims the Pawsey Stub requires the same adjustment for velocity factor. The electric and magnetic fields for the Pawsey Stub are outside the realm of the coaxial cable dielectric suggesting this is not the case.

I decided to research the literature and build working models of both to see for myself which Balun requires Velocity Factor correction.

First let’s examine the two Balun approaches and see what the literature suggests.

1:1 Coaxial Cable Balun

Figure 1 shows the pieces of this Balun…

This topology is brilliantly simple. A description can be found at I0QM’s web site PDF file[1].

Folded Balun

aka Pawsey Stub and 1/4 Wave Coaxial Balun
Figure 2 shows the idea behind the Pawsey stub which is known in Electrical Engineering circles as a variant of the Folded Balun[2].

While the Gray conductor in Figure 2 only needs to be a wire of similar size to the coaxial cable feedline, it is often made from a scrap piece of the same cable. Each end of the outer shield of the stub is connected to the feed system. A common thought of many is since this is coaxial cable, we need velocity factor adjustments. Since the electric and magnetic fields (of the stub system) are in air, I think velocity factor does not apply.

Figure 3 highlights my reasoning…

Figure 3a shows the construction of coaxial cable we are all familiar with. In normal operation all electric and most of the magnetic fields are contained between the inner and outer conductors. Since the spacing between these conductors is maintained by an insulating material, the fields are completely dependent on the dielectric constant of this material.

Figure 3b shows the same coaxial cable, but this time there are two pieces side by side as used in the Folded Balun. This balun, essentially a parallel transmission line, develops all its fields between the outer skin of the cables’ shields, not within. The stub wire, as used in the Pawsey Stub method, could be a copper wire with the same effect.

The studious reader will notice the external fields are not entirely in free air. The cable jacket certainly has a dielectric constant greater than 1 and, as thin as it is, will retard the speed of light a bit. The effect is much less than the situation inside coax, however. So… the VF of free air is not quite 1, but almost is… about 0.90 to 0.98 or so.

UPDATE Oct 2010:
Measurements made on a variety of Folded Balun test samples reveal the Velocity Factor actually varies from 0.7 to over 1 depending on cable type. Velocity factor over 1 is obviously impossible and suggests the real end points of the stub are slightly different from where I thought they were. Nonetheless, no external velocity factor measurement matched the easily verified internal Velocity Factor caused by the dielectric inside the coax. The spacing between the two conductors had an enormous impact on the final tuning point. The range of values was a surprise to this author. Details on these tests will be available in an upcoming post.

Other Views on Velocity Factor and Coax

Balanis discusses the theory behind matching techniques including the 1/4 Wave Coaxial 1:1 Balun. In particular he describes the purpose of the electrical short of the coax center conductor to shield, is to maintain balance, thereby, ensuring no current flows back to the transceiver on the outside of the coax. Interestingly, he notes…

“The parallel auxiliary line need not be made 1/4 wave in length to achieve the balance. It is made 1/4 wave to prevent the upsetting of the normal operation of the antenna.”[3]

The above point suggests a stub with incorrectly calculated lengths effectively quells unbalanced feedline currents (good) while corrupting the balance in the antenna (bad). It appears easy to be lured into a false sense of security.

The Pawsey Stub approach is nothing new. For decades the Stub Balun has been described in the various editions of the ARRL Antenna Book. The 21st edition describes a Sleeve Balun and the Stub Balun and suggests each is to be 1/4 wavelength. It does not mention anything about velocity factor corrections leaving the reader to wonder.[4]

Go back in time and we find the 13th edition of the ARRL Antenna Book says this about the stub approach…

“In either case, the length of the detuning element is a full quarter wavelength; the propagation factor of the line does not enter into the picture here.”[5]

Yet another view is noted by Roberts while describing his Wide-Band Balun named for him[6] stating about how long to make the parallel sections of coax thus…

“The length of the parallel section, measured from the point [. . .] where the two braids are connected together, to the points [. . .] where the balanced circuit is to be connected, is made one-quarter wavelength at the center frequency of the operating range. For the determination of this length, it is necessary to take account of the propagation velocity, which is somewhat higher than that of the waves moving along the inside of the coaxial cables.”[6]

Roberts recognized the fields of the parallel portion of his design are in a mix of free air and sheath dielectric. He goes on…

“Because of variations in composition, diameter, or eccentricity of the outer insulation, the characteristics of parallel lines formed from certain coaxial cable samples may differ appreciably from the desired value. It is generally necessary, therefore, to determine the characteristic impedance and velocity of propagation by testing sample parallel line sections made of the intended material.”[6]

Heeding Roberts’ warning and evaluating the other evidence above, I assert the published values of velocity factor of coaxial cable should not be used for stub length calculations for stubs with fields outside the cable’s interior.

Am I right? Let’s quit guessing and test it!

Part 2 of this series highlights the actual test I performed to prove I am correct.

References:

1. I0QM. “Coaxial Balun by I0QM.” http://www.iw5edi.com/ham-radio/files/I0QM_BALUN.PDF, 2001.
2. Milligan, Thomas. Modern Antenna Design. McGraw-Hill, Inc., 1985, pp. 74-77.
3. Balanis, Constantine. Antenna Theory – Analysis and Design. John Wiley & Sons, Inc., 1982, pp. 365-368.
4. R. Dean Straw et al. “Baluns and Antenna Tuners.” ARRL Antenna Book. The ARRL, Inc. 21st ed. 2007. pp 18.6-18.7.
5. Gerald L. Hall et al. “Using Coaxial Lines” ARRL Antenna Book. The American Radio Relay League, Inc. 13th ed. 1974. pp 229-230.
6. Proceedings of the IRE, “A New Wide-Band Balun,” Proceedings of the IRE, Volume 45, Issue 12, December 1957, pp 1628-1631